The Voter Model: An Introduction
The voter model is a mathematical model which describes the formation of opinions, attitudes or cultural attributes through social contact. It models how randomly chosen agents come into contact with neighbours and how they adopt or reject those neighbours’ attitudes or cultural characteristics such as political opinions or musical tastes.
In 1964, geneticists Kimura and Weiss [1] introduced the stepping stone model. This was developed by other geneticists over twenty years. It was subsequently discovered and named the voter model by probability theorists Clifford and Sudbury [2] in 1973 and Holley and Liggett [3] in 1975. Since then, it has been adapted and extended for a wide variety of contact process applications.
The voter model can be used to simulate and consider a broad range of emergent phenomena, including human social interaction. The model generates structured output from a given random input. The output can be visualised in agent-based form using cellular automata, coloured cells representing agents which may change shape or colour over time as they come into contact with neighbouring cells. Probabilistic rules are assigned to the behaviour of agents, their movements and how and with whom they interact over time. Since the physical status, colour or shape, of each cellular automaton indicates the agent’s current set of attitudes or characteristics, we can analyse how contact with a neighbour or neighbours affects them over time. For example, they may or may not imitate the majority around them.
In some computational models, the actions of agents are simultaneous and in others they are asynchronous. For asynchronous actions an activation order for agents must be decided. Agents could simply take actions randomly, or according to their geographical coordinates, movements, the number of neighbouring agents or certain endogenous characteristics such as age, propensity to conform, or incentive to act.
When talking about social systems, it is important to avoid strict determinism. Randomness is also important since it can help us account for very human aspects of decision making, such as making mistakes, the desire to experiment or the influence of personal bias. It should be noted that “randomness” is not synonymous with random behaviour. In a language competition model adding such probabilistic random noise might mean that an agent mistakenly assumes a neighbour speaks their language. Agents are more likely to make such mistakes when surrounded by others who do not share their characteristics.
Since interaction between speakers of different languages is one of the specific themes of this research project we might take a closer look at some existing voter models of language competition:
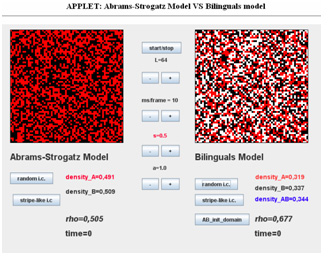
The Abrams-Strogatz model [4] is a model for the dynamics of endangered languages and addresses competition between two languages. In this model an individual within a network can be in two possible monolingual states: A speaker of one language (A) or a speaker of another (B).
The agent’s status or rather change of status depends on the density of speakers of each language in the surrounding local community, the social prestige of each language and the volatility (inertia or propensity of the agent to change language).
The Minett-Wang model [5] extends this model to take account of bilingualism. Agents can therefore speak one language (A or B) or be in a bilingual state (AB) and so the three rather than two local densities for each state must be considered in relation to each agent (node).
Equations allow us to calculate various probabilities on the basis of these densities, the prestige of each language and the volatility: The probability of a monolingual agent (A or B) moving to the bilingual community and the probability of a bilingual agent (AB) moving to the monolingual (A or B) community. When an agent changes state from one monolingual state to the other (A to B or B to A) the agent passes through an intermediate AB state.
The Abrams-Strogatz model and the Minett_Wang model (Cellular Automata: Screen capture of applet [6])
In 2006, Castelló, Eguíluz, and San Miguel [7] proposed another 3-state extension of the voter model concerning language competition. The specific aim of this model was to explore possible mechanisms which might lead to a state of stable co-existence, or meta-stable states, rather than the eventual dominance (or extinction) of one language. They paid particular attention to the role of bilingual agents and social structure, including small world phenomena due to communication and interaction between geographically distant agents, in complex networks.
Conclusions
The voter model is particularly relevant to our research themes: The visualisation and analysis of social interaction, emergence and their relation with social consensus. As a visualisation tool, such models permit the analysis of unfolding events both in real time and retrospectively. We can also retrace the movements and actions of agents as required.
However, we must be cautious. Such computational models do not actually represent social phenomena or observed social behaviour.
In the voter model, consensus is said to be reached when a model arrives at an “absorbing” (constant) state. Although different initial conditions and applied rules affect the outcome, the result is always consensus in the end. In language competition models, for example, one or other language always prevails. Thus, consensus is defined as a stable block of agreement. The relationship between this conceptualisation and the philosophical concept of meta-stability should later be examined.
Other models do not necessarily lead to an “absorbing” state. In 1997, Axelrod [9] proposed a model on cultural dissemination in which, as in the voter model, agents’ characteristics or traits converge as a result of concrete social interaction. Agents also tend to interact with those most similar. However, the model concluded that, on a global level, we are tending towards a state of multiculturalism (polarisation), rather than convergence. These and many other models have been developed to describe social networks and will be duly discussed.
- M. Kimura and G. Weiss. The Stepping Stone Model of Population Structure and the Decrease of Genetic Correlation with Distance. Genetics. 49(4):561–576, 1964.
- P. Clifford and A. Sudbury. A model for spatial conflict, Biometrika, 60(3):581-588, 1973.
- R. A. Holley and T. M. Liggett. Ergodic theorems for weakly interacting infinite systems and the voter model, Annals of Probability, 3:643-663, 1975.
- D. M. Abrams and S. H. Strogatz. Modelling the dynamics of language death, Nature 424: 900 (2003).
- W. S-Y. Wang and J. W. Minett, The invasion of language: emergence, change and death, Trends in Ecology and Evolution, vol. 20, pp. 263–269, 2005.
- http://ifisc.uib.es/eng/lines/complex/APPLET_LANGDYN.html
- X. Castelló, V. M. Eguíluz, and M. San Miguel, Ordering dynamics with two non-excluding options: bilingualism in language competition, New Journal of Physics, vol. 8, pp. 308–322, 2006.
- J. H. Miller and S. E. Page, Complex Adaptive Systems. An Introduction to Computational Models of Social Life, Princeton University Press, Princeton and Oxford, 2007. p. 124-129.
- R. Axelrod, “The dissemination of culture: A model with local convergence and global polarization,” The Journal of Conflict Resolution, vol. 41, no. 2, pp. 203–226, 1997.